Conservation of Rotational Kinetic Energy
The total I is four times this moment of inertia because there are four blades. A Figure Skater - Revisit.
What Is The Ratio Of Rotational Kinetic Energy To The Total Kinetic Energy Of A Hollow Sphere Quora
Calculate rotational kinetic energy.
. A rolling object possesses kinetic. Kinetic energy KE in rotational motion is related to moment of rotational inertia I and angular velocity ω. Here are a few examples that will clarify what rotational kinetic energy RKE is-.
The problems can involve the following concepts 1 Kinetic energy of rigid body under pure translation or pure rotation or in general plane motion. The equation we used previously for kinetic energy is K ½ mv2. Flywheels for example can be used to store large amounts of rotational kinetic energy in a vehicle as seen in Figure 3.
The moment of inertia of one blade is that of a thin rod rotated about its end listed in Figure 1020. The extended objects complete kinetic energy is described as the sum of the translational kinetic energy of the centre of mass and rotational kinetic energy of the centre of mass. The rotational kinetic energy is related to the rotational inertia and the square of the angular velocity magnitude.
There are several references to lost kinetic energy when trying to analyze motion based on the Conservation of Momentum and the Conservation of Energy laws. Work and energy in rotational motion are completely analogous to work and energy in translational motion first presented in Uniform Circular Motion and Gravitation. Energy possed by the ceiling fan because of its rotary motion.
Conservation of Energy Rotational Dynamics. If you were to lift the front wheel of the bike and spin it while the bike is stationary then the wheel would have only rotational kinetic energy relative to the Earth. ω 300 rev 100 min 2 π rad 1 rev 100 min 600 s 314 rad s.
In physical sciences mechanical energy is the sum of potential energy and kinetic energyThe principle of conservation of mechanical energy states that if an isolated system is subject only to conservative forces then the mechanical energy is constantIf an object moves in the opposite direction of a conservative net force the potential energy will increase. But rotational kinetic energy is proportional to the moment of inertia now one quarter of its initial value times. And if the speed not.
Nomy previous comments applied to the charging of a fixed capacitor where when Q increases then so does V in direct proportion QCVAs far as the energy equation is concerned make your choice. This work goes to increasing the rotational kinetic energy. The kinetic energy is generated by an objects rotation which is a component of its overall kinetic energy.
Equivalent of translational kinetic energy. Both masses will rotate with. Similarly even in rotational motion KE is conserved and it is known as rotational kinetic energy.
The objective of this experiment is to study the law of conservation of energy and some concepts of rotational dynamics. A variety of problems can be framed on the concept of rotational kinetic energy. Here the energy changes into heat when friction.
2 V R w. Recall that the rotational kinetic energy of an object is. The kinetic energy of a purely rotating object is thus given by.
Figure 1 shows a worker using an electric grindstone propelled by a motor. Rotational kinetic energy has important effects. Sparks are flying and noise and vibration are created as layers of steel are pared from the pole.
3 Conservation of mechanical energy. 2 Work done by torque and its relation with rotational kinetic energy in case of fixed axis rotation. Just as in translational motion where kinetic energy equals 12mv 2 where m is mass and v is velocity energy is conserved in rotational motion.
We know that kinetic energy is conserved in translational or linear motion and we find out using the formula KE 12mv2. Thus I 4 M l 2 3 4 500 kg 400 m 2 3 10670 kg m 2. The expression for rotational kinetic energy is exactly analogous to translational kinetic energy with I being analogous to m and ω to v.
This confirms that the work done went into rotational kinetic energy. The MG converts energy between mechanical and variable-frequency electrical. An MG and power electronics.
The thing which stays the same is the capacitance C so the energy is 12 CV2. Rotational kinetic energy is the energy possessed by the object due to its rotational motion OR in other words we can say that it is the kinetic energy of a rotating object. Demonstrate the Law of Conservation of Energy.
The terms in brackets are the same so the final kinetic energy is larger than the initial kinetic energy because. When the flywheel is used as a mechanical battery energy must be converted from rotational kinetic energy to usable electrical power and vice versa. It must stay the same because of conservation of energy.
Also the linear velocity relates to the angular velocity by. The rotational motion of the tire means it has rotational kinetic energy while the movement of the bike along the path means the tire also has translational kinetic energy. We will apply the relationship between the potential energy and kinetic energy of a spherical object rolling without slipping down a ramp.
Since the product of moment of inertia and angular velocity must be conserved moving so that you are half as far from the center will quadruple the angular velocity. In this module we will learn about work and energy associated with rotational motion. None of these.
Generally the answer to apparent discrepancies include references to elastic or in-elastic collisions and whether or not they are perfect. We can find the equivalent expression for kinetic energy in a rotational setting by replacing mass m by rotational inertia I and speed v by angular speed. Kinetic energy is even conserved in the rotational motion of an object.
Happens to the skaters rotational kinetic energy. This conversion usually involves two major components. The total energy of a system can be subdivided and classified into potential energy kinetic energy or combinations of the two in various.
A ball rolling down a hill an. 1 KErot 5 I w2 in which w is the angular velocity and i5 M R2 is the moment of inertia about the cm. Where does the extra kinetic energy come from.
Now we solve one of the rotational kinematics equations for αθ. This video goes over rotational kinetic energy and how to use conservation of energy to solve for two classic physics problems.
Ela Component Mass Distribution And Rotational Inertia

Question Video Calculating The Rotational Kinetic Energy Of A Football Nagwa

Conservation Of Energy Including Rotation Youtube
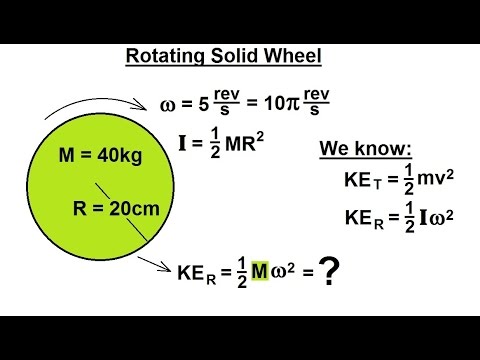
Physics 8 5 Rotational Kinetic Energy 1 Of 19 Rotating Solid Disk Youtube

Rotational Kinetic Energy And Moment Of Inertia Examples Physics Problems Youtube

Rotational Kinetic Energy Review Article Khan Academy
0 Response to "Conservation of Rotational Kinetic Energy"
Post a Comment